Statistics

Understanding the Measure of Central Tendency: A Friendly Guide to Calculating the Mean

Statistics can feel like a maze sometimes, but the mean? That’s your trusty compass. It’s just the average of a data set—a simple way to find the central point of your numbers. I’ve always found it handy, whether I’m summarizing data as a data scientist or figuring out my monthly coffee spending (which, trust me, once got skewed by a fancy latte spree!). Let’s dive into what the mean is, how to calculate it, and when it’s the right tool for the job. I’ll toss in some examples and tips to make it stick—all in a way that feels like a chat over coffee, not a lecture.

What’s the Mean, Anyway?

The mean is the average you probably learned in school: add up your numbers, divide by how many you’ve got, and there’s your center. It’s perfect for getting a quick sense of what’s typical—like the average time users spend on an app or my usual coffee splurge (don’t judge!). It’s one of the most common measures of central tendency, and for good reason: it’s straightforward and gives you a solid starting point.

How to Calculate the Mean: Easy as Pie

Here’s the no-fuss way to find the mean:

  1. Add up all the values in your data set.
  2. Count how many values you have.
  3. Divide the sum by the count.

Let’s put it into formulas so it’s official:

  • Sample Mean:
    \overline{x} = \frac{\sum{x}}{n}
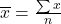
    “x-bar” is the sample mean, “sum of x” is the sum of your data points (think x1 + x2 + … + xn), and “n” is the number of items.
  • Population Mean:
    \mu = \frac{\sum{x}}{N}
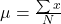
    Here, “mu” is the population mean, and “N” is the total data points in the whole group.

Example 1: My Coffee Spending

Picture this: last week, I spent $5, $10, $8, and $5 on coffee. (Yes, I’m a creature of habit.) Here’s how I’d find the mean:

  • Add them up: 5 + 10 + 8 + 5 = 28
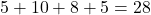
  • Count the days: 4
  • Divide: \frac{28}{4} = 7

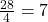
So, my average coffee spend was $7 per day. Makes sense—most days were around that mark!

Example 2: User Session Times

Imagine I’m analyzing user session times on a website: 70, 75, 72, 68, and 95 seconds (someone got hooked!). Here’s the mean:

  • Sum: 70 + 75 + 72 + 68 + 95 = 380
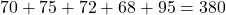
  • Count: 5
  • Divide: \frac{380}{5} = 76

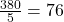
The mean session time is 76 seconds. That 95 pulls it up a bit—something to watch for later.

Example 3: When Outliers Sneak In

One time, I tracked my daily steps: 5,000, 6,000, 5,500, and 20,000 (a hiking day!). Let’s calculate:

  • Sum: 5,000 + 6,000 + 5,500 + 20,000 = 36,500
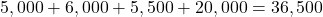
  • Count: 4
  • Divide: \frac{36,500}{4} = 9,125

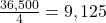
Average steps: 9,125. But most days were closer to 5,000-6,000. That 20,000 skewed things—a classic outlier mess!

When the Mean Works Like a Charm

The mean shines when your data is balanced. My coffee spending? Pretty steady, so $7 feels right. Same with the session times (mostly 68-75)—76 seconds reflects the group well, even with that 95. It’s quick, professional, and gives me a solid number to plug into a report or model.

When to Ditch the Mean

Here’s where it gets tricky—and personal. That time I used the mean for my steps? Disaster. The 20,000-step hike threw off the average, making it useless for my typical day. Same with some income data I once analyzed: $30k, $35k, $40k, and $1 million. Mean? $276,250. Reality? Most folks weren’t millionaires!

  • Outliers: Extreme values (like 20,000 steps or $1 million) distort the mean.
  • Skewed Data: When numbers lean one way (like incomes or wait times), the mean misleads.

In those cases, I lean on the median—the middle value. For my steps, it’s 5,750—way more realistic. It’s a lesson I learned after overfitting a model to a wonky average!

Why This Matters (From a Data Scientist’s Desk)

As a data scientist, I lean on the mean constantly—think aggregating user metrics, forecasting trends, or summarizing model outputs. It’s a workhorse in my toolkit. But knowing its limits keeps me honest. Outliers and skew can throw off your analysis, and I’ve seen teammates stumble over this in dashboards or client reports. Whether you’re wrangling data for a living, studying stats, or just poking around numbers for fun, picking the right measure—mean or otherwise—ensures your insights hold water.

Key Takeaways to Nail the Mean

  • It’s the average: sum divided by count (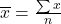\overline{x} = \frac{\sum{x}}{n} or \mu = \frac{\sum{x}}{N}).
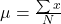  • Great for balanced data—like my $7 coffee habit.
  • Skip it when outliers (like 20,000 steps) or skew mess things up—try the median.
  • Practice it: coffee, session times, steps—whatever numbers you’ve got lying around!

Your Turn to Crunch Some Numbers

I’ve shared my coffee woes and data tales—now it’s your turn. Got a data set you want to average? Try it out and see if the mean fits. If it feels off, let me know—I’d love to troubleshoot it with you. Numbers don’t have to be intimidating; they’re just stories waiting to be told!